AP Syllabus focus:
‘Students interpret verbal descriptions by deciding which quantity depends on another, naming the independent and dependent variables, and expressing their relationship using derivative notation in a differential equation.’
Identifying dependent and independent variables is essential for translating real-world descriptions into differential equations that accurately represent how one quantity changes in response to another.
Understanding Variable Roles in Context
In many applied situations, students must determine how a described quantity behaves and which measurement provides the reference against which change is evaluated. A dependent variable is the quantity whose value changes as another quantity varies, while the independent variable is the one that drives or indexes this change.
This graph illustrates a generic function , showing the independent variable on the horizontal axis and the dependent variable on the vertical axis. The highlighted point emphasizes how each input corresponds to an output. The marked values are additional details beyond the syllabus but reinforce the dependency relationship. Source.
Dependent Variable: The quantity whose value depends on changes in another quantity and is typically represented as a function of the independent variable.
A verbal description might describe how a population changes over time, how temperature changes with distance, or how a chemical quantity changes as a reaction proceeds. In each case, understanding which quantity is influenced and which serves as the controlling measure is the foundation for writing meaningful derivative expressions.
Recognizing Independent Variables in Verbal Descriptions
The independent variable is usually a quantity such as time, position, or another measurable input that provides a natural axis of change. Students should look for cues in wording including “as time passes,” “with increasing distance,” or “as x increases,” which signal which variable serves as the baseline of reference.
Independent Variable: The quantity that acts as the input of a function and with respect to which change in the dependent variable is measured.
A sentence describing a rate like “the rate of change of the temperature as you move along the rod” implies that the temperature depends on position, making position the independent variable. If a verbal statement involves how quickly something “grows per year,” time is almost always the independent variable.
A clear identification of the independent variable ensures the derivative notation or aligns with the context. Choosing incorrectly can lead to misinterpretation of the modeled behavior.
Establishing the Dependent Variable Through Context
Once the independent variable is determined, the dependent variable is the quantity being monitored or predicted. It is often introduced as the amount, size, or value being described. Phrases such as “the population increases,” “the height decreases,” or “the concentration changes” indicate the dependent variable because they describe what is undergoing variation.
Students should confirm that the dependent variable represents a function whose changes are dictated by the independent variable. For instance, a statement like “the velocity of the object depends on time” frames velocity as the dependent variable and time as the independent variable.
Connecting Variables to Derivative Notation
Once variable roles are identified, the differential equation is expressed using derivative notation to reflect how the dependent variable changes with respect to the independent variable. This notation is a mathematical translation of statements involving “rate of change,” “increase proportionally,” or “changes at a rate equal to.”
= Dependent variable representing the changing quantity
= Independent variable representing the measure against which change is evaluated
This symbolic expression condenses the contextual description into a form that can be analyzed, solved, or interpreted. Students should ensure the derivative aligns with the structure of the sentence, particularly the direction of dependency.
A well-chosen derivative expression also supports later verification, modeling, and solution procedures by preserving the intended relationship between variables.
Strategies for Identifying Variables in AP-style Contexts
Students can adopt several reliable strategies when analyzing contextual descriptions:
Highlighting Situational Keywords
Look for linguistic markers that indicate dependency. Phrases such as:
• “depends on”
• “changes with”
• “as ___ increases”
• “rate of change of ___ with respect to ___”
These expressions typically point to the correct orientation of the variables. The first blank is usually the dependent quantity, and the second blank identifies the independent variable.
Considering Units and Measurement
Units provide powerful clues about variable roles. When a rate is expressed in units like “meters per second,” the numerator represents the dependent quantity, and the denominator indicates the independent variable.
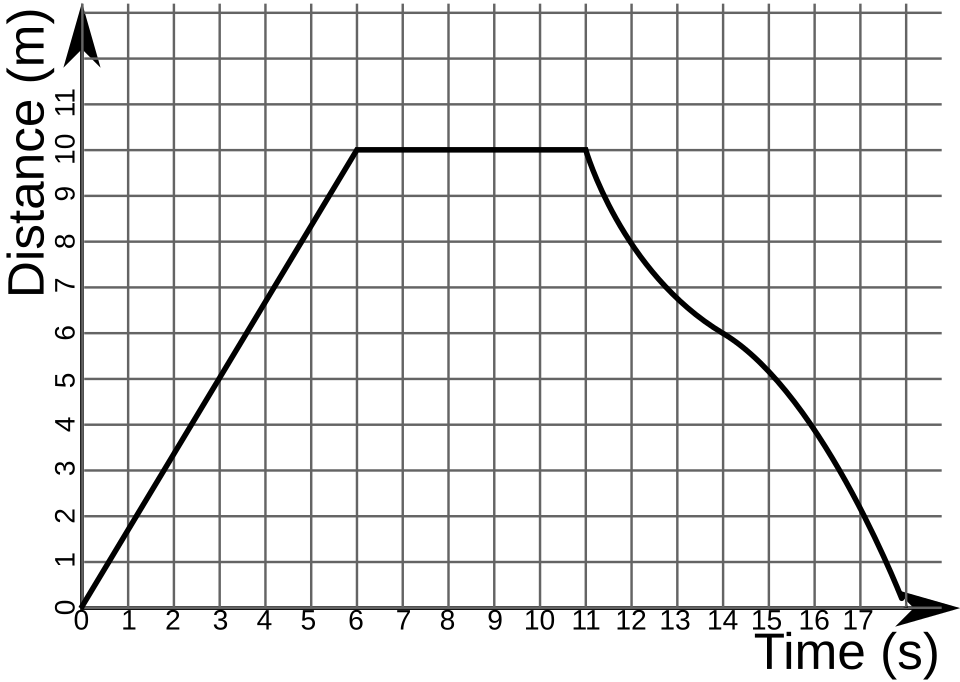
This distance–time graph places time on the horizontal axis and distance on the vertical axis, showing how the dependent variable changes as the independent variable increases. The curve indicates non-constant change in distance over time. The gravitational context on the original page exceeds the syllabus scope but still reinforces variable roles. Source.
Aligning Variables With Modeling Intent
Students should ask what the problem ultimately wants them to determine or predict. The target quantity almost always serves as the dependent variable. If a scenario aims to predict population over time, population is the dependent variable; if it aims to understand temperature variation along a rod, position becomes the independent variable.
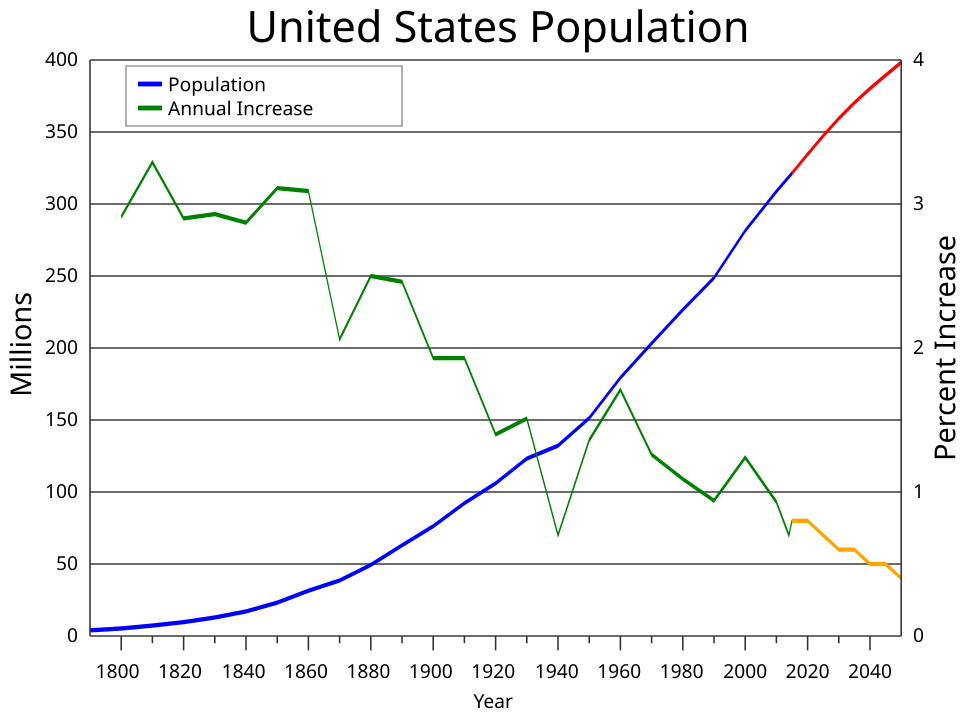
This graph displays population as a function of time, demonstrating a dependent variable whose value changes with the independent variable. The rising curve highlights long-term trends in growth. The detailed census projections exceed syllabus needs but clearly illustrate dependency on time. Source.
Ensuring Consistency With Functional Thinking
In any differential equation, the dependent variable must be a differentiable function of the independent variable. Students should mentally test statements like “y is a function of x” or “y changes as x changes” to verify logical alignment before writing derivative notation.
Understanding how to identify dependent and independent variables empowers students to translate real-world descriptions accurately and to express these relationships clearly using differential equations.
FAQ
Look for the quantity being described as changing, increasing, decreasing, or responding to something else. This is almost always the dependent variable.
Phrases such as “varies with”, “responds to”, or “changes as” generally indicate the direction of dependency. The variable appearing after “with respect to” is typically the independent variable.
Reversing roles leads to an equation that expresses the wrong dependency, which can change the meaning of the entire model.
It also affects:
• the correct derivative notation,
• the interpretation of units,
• and the validity of later solution methods such as separation or slope-field analysis.
Yes, particularly in modelling contexts where multiple quantities vary in predictable ways.
However, only one choice typically aligns with the wording. If both time and position change, time is usually preferred because it provides a natural and universally understood direction of change.
Only choose alternatives when the context explicitly frames the variable relationship differently.
Rates written in compound units such as “grams per minute” or “litres per kilometre” reveal the denominator as the independent variable.
The numerator indicates what is changing, while the denominator indicates the quantity against which this change is measured. Units therefore provide a reliable secondary check when the wording is ambiguous.
Look for subtle clues such as which quantity is being predicted, measured, or tracked. That quantity is typically dependent.
If uncertainty remains:
• Identify which variable could sensibly be expressed as a function of the other.
• Choose the variable that naturally progresses or acts as an index as the independent variable.
This approach ensures the model reflects realistic behaviour even without explicit statements.
Practice Questions
Question 1 (1–3 marks)
A tank contains a chemical solution whose concentration changes as time passes. A description states:
“The rate of change of the concentration depends on time.”
(a) Identify the independent variable.
(b) Identify the dependent variable.
(c) Write the appropriate derivative notation expressing how the concentration changes with respect to time.
Question 1 (3 marks total)
(a) Independent variable: time.
• 1 mark for correctly identifying time.
(b) Dependent variable: concentration.
• 1 mark for correctly identifying concentration.
(c) Appropriate derivative notation: dC/dt or similar.
• 1 mark for correct notation showing concentration differentiated with respect to time.
Question 2 (4–6 marks)
A researcher studies how the temperature along a metal rod varies with distance from one end. The description states:
“The temperature at a point depends on the distance x from the left end of the rod, and the rate of change of temperature with respect to distance is given verbally by the model.”
(a) State the independent and dependent variables, explaining your reasoning.
(b) Write the derivative notation that represents the rate of change of temperature with respect to distance.
(c) The researcher later claims that distance depends on temperature instead. Explain why this interpretation is inconsistent with the given context.
Question 2 (6 marks total)
(a) Independent variable: distance x.
Dependent variable: temperature.
Reasoning: temperature changes as distance changes along the rod.
• 1 mark for identifying distance as independent.
• 1 mark for identifying temperature as dependent.
• 1 mark for explanation linked to “temperature depends on distance”.
(b) Derivative notation: dT/dx or equivalent.
• 1 mark for correct derivative form.
(c) Explanation: The description explicitly states that temperature varies according to position along the rod, so position determines the temperature value, not vice versa. Claiming distance depends on temperature reverses the stated dependency and contradicts the modelling description.
• 1 mark for identifying the contradiction with the context.
• 1 mark for clearly explaining why reversing dependency is inappropriate.

